refere[4ces

[ I] R.D. MlDDLEBROOK, Low Entropy EKptessions: The Key to Design-Oriented Analysis, IEEE Frontiers

in Education Conference, 1991 Proceedings, pp. 399403, Sept. 1991.

[2] R. D. MlDDLEBROOK, Methods of Design-Oriented Analysis: The Quadratic Equation Revisited, IEEE

Frrmtiers in Education Conference, 1992 Proceedings, pp. 95-102, Nov. 1991.

[3] F. B.eizeoar, S. Cuk. and R. D. MiDDLEEEiOOK, Using Small Computers to Model and Measure Magni-

tude and Pha.se of Regulator Transfer Functions and Ump Gan, Froceeilings (}f Ptjweicon S, April 1981. Also in Advances in Switciied-Mode Power Conversion. Irvine: Teslaco, Vol, I, pp. 251-278, 1981,

[4] H. W. Ott, Noise Reduction Teclniiqites in Electronic Systems, 2nd edit., .New York: John Wiley & Sons,

1988, Chapter 3.

Problems 8.1

Express (he gains represented by lhe asymptoles of Figs. 8.62(a) 10 (c) in factored pole-zero fiiiin. You may assume that all poles and zeroes have negative teal parts.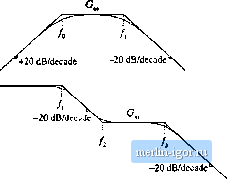

/[-20 dB/decade +20 dB/deeade

Fig. 8.62 Gain asymptotes for Pmblcin 8,1.

8J Express the gains represented by the asymptotes of Figs. 8.63(a) to (c) in factored pole-zero form. You

may assume that all poles and zeroes have negative real parts.

S.3 Derive analytical expressions for the low-frequency asymptotes of the magnitude Bode plots shown in

Fig, S.63(a) to (c),

8J Derive analytical expressions for the three magnitude asymptotes of Fig, 8,16.

+20 dB/decade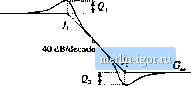

20 dB/decade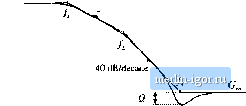

Fig. S.63 Gain aNyinpfotes ior Problems 8,2 and 8.3.

8.5 An experimenlally measured iransfer Tunulion. Figure 8.64 uonlains experimenlally measured magni-

lude and phase duLa for (he gain function A(.f) of a certain amplifier. The object of this probleni is to find an expression forAtj). Overlay asymptotes appropriate on the magnitade and phase data, nd hence deduce numerical values tor the gain asymptotes and corner frequencies of Your magnitude and

40 dB

30 dB

20 dB

10 dB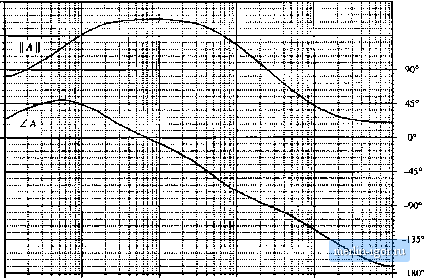

10 Hz

too Hz

1 kHz

10 kHz

100 kHz

1 MHz

Fig. 8.64 ExpcrimentaHy-incitsured magnitude and phase data. Pi-oblem

phase asymploles musl, of course, follow all of lhe rules: magnilude slopes musl be makiples of ±20 dB per decade, phase slopes for real poles musl be mutuples of ±45° per decade, eLc. The pha.se and magni-(ude asymptotes must be consistent wilh each other.

It is suggested that you start by guessing А(.т) based on the magnitude data. Then construct the phase asymptotes for your guess, and compare them with lhe given data. Iflhere are discrepancies, then modify your guess accordingly and redo your magnitude and phase asymptotes. You should turn in: (1) your analytical e?:pression for A(s). wilh numerical values given, and (2) a copy of Fig, S.64, with your magnitude and phase a.symptotes superimposed and wilh all break frequencies and slopes clearly labeled.

SjS An experimentally-measured impedance. Figure 8.65 contains experimentally measured magnitude and

phase data for the driving-poinl impedance Z(s) of a passive network. The object of this problem is the find an expression for Z(s). Overlay asymptotes as appropriate on the magnitude and phase data, and hence deduce numerical values for the salient features of the impedance function. You should turn in: (1) your analytical expression for ZfO, wdlh numerical values given, and (2) a copy of Fig. 8.65, wilh your magnitude and phase asymptotes superimposed and wilh alt salient features and asymptote slopes clearly labeled.

30 dBQ

20 dBQ

Fig. 8,65 Impedance tnagni-tude and phase data, Froblem 8.6.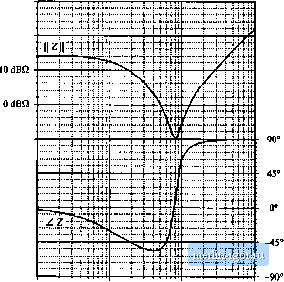

-lOdBn

to Hz

100 Hz

1 kHz

10 kHz

8.7 In Section 7.2.9, the small-signal ac model of a nonideal flyback converter is derived, wilh the result illiistraled in Fig. 7.27. Construct a Bode plot of the magnitude and phase of the converter output impedance Z, ,(j-). Give both analytical expressions and numerical values for all important features in your plot. Note: Zis) includes the load resistance R. The element values are: D = 0.4, n ~ 0.2, Д = й i2, L = 600 fiU, С = 100 fiK, Л = 5 Q.

8.8 For the nonideal flyback converter modeled in Section 7.2.9:

(a) Derive analytical expressions for the control-to-oulput and line-to-output transfer functions G/,s) and G.(.v). Express your results in standard normalized form.

(b) Derive analytical expressions for the salient features of tbese transfer functions.

(c) Construct the magnitude and phase Bode plots of lhe control-to-output transfer function, using