This page intentionally left blank

Basic Magnetics Theory

Magnetics are an integral part of every switching converter. Often, the design of the magnetic devices cannot be isolated from the converter design. The power electronics engineer tntist not only model and design the converter, but must model and design the magnetics as well. Mtxieling and design of magnetics for switching converters is the topic of Part III of this book.

In this chapter, basic tmgnetics theory is reviewed, including magnetic circuits, inductor modeling, and transformer modeling [1-5]. Loss mechanisms in magnetic devices are described. Winding eddy currents and the proximity effect, a significant loss mechanism in high-current high-frequency windings, are explained in detail [6-11]. Inductor design is introduced in Chapter 14, and transformer design is covered in Chapter 15.

13,1 REVIEW OF BASIC MACJINETICS 13.1.1 Basic Relationships

The basic magnetic quantities are illustrated in Fig. 13.1. Also illustrated are the analogous, and perhaps more fatniiiar, electrical quantities. The magrturomorive force or scalar potential, between two points x and Xj is given by the integral of the magnetic fteld H along a path connecting the points:

fpn-dl (13.1)

where dt is a vector length element pointing in the direction of the path. The dot product yields the com-

Basic Maguesics Theory

Magnetic quantities

Electrical quantities

Length e

Magnetic field И

- Length e-

Electnc field E

MMF -.iJ= Hi

Voltage

Total flux Ф Flux density В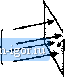

Surface S wilh агеаЛ

Total current / Current density /

Surface 5 with area

Fig, 13.1 Comparison of magnetic field И, MMP Ф, flux and (lux density B, wiih the aiialiious electrical quaii-titiesi E, V; /, tind J.

ponent of H in the direction of the path. If the magnetic field is of uniform strength H passing through an element of length t as illustrated, then Eq. (1 L1) reduces to

03.2)

This is analogous to the electric field of uniform strength £, which induces a voltage V = £f between two points separated by distance L

Figure 13.1 also illustrates a total magnetic flux Ф passing through a surface S having area Л.. The total flux Фis equal to the integral of the normal coraponeut of the flux density В over the surface

(13.3)

where dA is a vector area element having direction normal to the surface. For a uniform flux density of magnitude В as illustrated, the integral reduces to

Ф = аА,.

(13.4)

Flux density В is analogous to the electrical current density / and flux Ф is analogous to the elechic current /. If a uniform current density of magnitude / pas.ses through a surface of area then the total current is / = JA.

Faradays law lelate.s the voltage induced in a winding to the total flux passing dirough the iute-rior of the winding. Figure 13.2 illustrates flux Ф(() passing through the interior of a loop of wire. The loop encloses cross-sectional area /1. According to Faradays law, Ihe flux induces a voltage v(t) in the wire, given by

K0 =

(13,5)

where the polarities of v(f) and Ф(() are defined according to the right-hand rule, as in Fig. 13.2. For a