Core

Primary winding Secondary winding

Ф 2Ф ЗФ 2Ф Ф

®

® -i 2i

Current

density J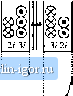

-2; 1

®

I.

Primary windiitg

rff-

CM i i

Secondary winding

Pig. 13,25 A siinpls transformer example illuslrating the proximity cdta: (u) core atid windijig geometry, (b) distribution of currems oti surfaces of conductors.

in Fig. 13.25. Hence, current - i(r) Hows on the left surface of the second layer. Since layers 1 and 2 are connected in series, tlicy must botli conduct tlie same net current if/). As a result, a ctirrent + 2;(f) must flow on the right-side surface of layer 2.

The current tlowing on the left surface of layer 2 has the same magnitude as the current of layer l,and hence the copper Itj.ss is the sime: p The current flowing on the tight surface []f layer 2 has tins magnitude 21; hence, it induces copper loss (21 fP. =4P. The total copper loss in primary layer 2 is therefore

Л = f I + AP, = 5P

(13,64)

The copper loss in the second layer is five times as large as the copper loss in the first layer!

The current 2i(f) tlowing on the right surface of layer 2 induces a flux 2Ф([) as illustrated in Fig. 13.25. This causes an opptjsing current - 2!(f) to How on the adjacent (left) surface of primary layer 3. Since layer 3 must also conduct net cutrent /(f), a current + 3/(/) Hows on the right surface of layer 3. The total copper loss in layer 3 is

Likewise, the copper loss in layerm ot a tnttltiple-layer winding can he written

(13.65)

(13.66)

It can he seen that the copper loss compounds very quickly in a multiple-layer winding.

The total copper loss in the three-layer primary winding is Я, + Sfj + liP,ut ]9P. More generally, if the winding contains a total of M layers, then the total copper loss is

(13.67)

If a dc or low-frequency ac current of rms amplitude / were applied to the Л/-]ауег winding, its copper loss would be P = iMli. Hence, the proximity effect increases the copper loss by the factor

(13.6B)

Thi.s expression is valid for a foil winding having /1 э> ё.

As illustrated in Fig. 13.25, the currents in the secondary winding are symmetrica], and hence the secondary winding has the same conduction loss.

The example above, and the associated equations, are limited to A э> 5 and to the winding geometry shown. The equations do not quantify the behavior for Л - f>, nor for round conductors, nor are the equations sufficiently general to cover the more complicated winding geometries often encountered in the magnetic devices of switching converters. Optimum designs may, in fact, occur with conductor thicknesses in the vicinity of one penetration depth. The discussions of the following sections allow computation of proximity losses in tnore general circutnstances.

13.4.2 Leakage Flux in Wintlings

As described above, an externally-applied magnetic field will induce eddy currents to flow in a conductor, and thereby induce copper loss. To understand how magnetic fields arc oriented in windings, let us consider the simple two-winding transformer illustrated in Fig. 13.26. In this example, the core has large permeability /( fljj. The primary winding consists of eight turns of wire arranged in two layers, and each turn carries current /(f) in the direction indicated. The secondary winding is identical to the primary winding, except that the current polarity is reversed.

Flux lines for typical operation of this transformer are sketched in Fig. 13.26(b). As described in Section 13.2, a relatively large mutual flux is present, which magnetizes the core. In addition, leakage flux is present, which does not completely link both windings. Because of the symmetry of the winding geometry in Fig. 13.26, the leakage flux runs approximately vertically through the windings.

To determine the magnitude of the leakage flux, we can apply Atnperes Law. Consider the closed path taken by one of the leakage flux lines, as illustrated in Fig. 13.27. Since the core has large permeability, we can assume that the MMF induced in the core by this flux is negligible, and that the

Leakage jlixx

Mutual flux

Fig. 13.26 TVo-windiiig transformer example: (a) tore and winding geometry, (b) typical flux distribution.

total MMF around tlie path is dtuniiiated by the MMF l9{x) across the ctire window. Hence, Amperes Law states that the net cunent enclosed by the path is equal to the MMF itcross the iiir gap:

Encioseil current = .f{x) ~ .

(13.69)

where is the height of the window as shown in Fig. 13.27. The net current enclosed by the path depends on the number of primary and secondiuy conductors enclosed by the path, and is therefore a function ofthe hoiizontai posttitm л. The first layer ofthe primary winding consists of 4 turns, each carrying cuii-ent i(r). So when the path encloses only the first iayei- of the primai-y winding, then the enclosed current is 4((r) as shown in Fig. 13.28. Likewise, when the path encloses both layers ofthe primary winding, then the enclosed current is 8r(0. When the path encloses the entire primai, plus layer 2 ofthe secondary winding, then the net enclosed current is 8i(r) - 4/(r) = 4((/). The MMF {x) acr[)ss the core window is zero outside the winding, and rises to a maxiniuni of 8((/) at the interface between the primary and secondary windings. Since Я() = !{x}lt,, the inagnetic field intensity H{x) is proportional to the sketch of Fig. I3.2S.

Fig. 13.27 Analysis of leakage flux using Amperes Law, for the nransformer of Fig. 13,26.

Leakage path

®

Enclosed current