gl = 201o8, [61

(3.3) Table S.l Expiessitig magniiudes in tiecibels

Decibel values of some simple magnitudes are listed in Table 8.1. Care must be used when the magnitude is not dimensionless. Since it is not proper to take the logarithm of a quantity having dimensions, the magnitude must first be normalized. For exatnple, to express the magnittide of an impedance Z in decibels, we should normalize by dividing by a base impedance

2l = 20 log,

(Я.4)

The value of is arbitrary, but we need to tell others what value we have used. So if Z [ is 5 Й, and we chot)se R = 10 Si, then we can say that Z\\ = 20 log(,{5 ППШ) = - 6dB with respect to 10 tl, A common choice is Й;,., = 1Й; decibel impedances expressed with Rj,. = i Й are said to be expressed in dBi2. So 5 fi is equivalent to 14 dBQ. Current .switching harmonics at the input port of a converter are often expressed in dBiA, or dB using a base current of 1 f(A: 60 dBftA is equivalent to 1000 (A, or ImA,

The magnitude Bode plots of functions equal to powers of/are linear. For example, suppose that the magnitude of a dimensionless quantity (Jif) is

whereand n are constants. The magnitude in decibels is

G,5 = 201og,

= 2Qfi hig i

(8.5)

(8.6)

This equation is ploUed in Fig. 8.3, for several values of л. The magnitudes have value 1 => 0 dB at fre-q[iency/=/(J, They are linear functions of log[y(/). The slope is the change in G \\. arising from a unit change in logg(/); a unit increase in log[,(/) corresponds to a factor of 10, or decade, increase in /. From Eq. (8.6), a decade inctease in/leads to an increase in G j[Of 20и dB. Hence, the slope is 20k dB per decade. Equivalently, we can say that the slope is 2()ii 1о§[ц(2) = 6н dB per octave, where an octave is a factor of 2 change in frequency. In practice, the magnitudes of most frequency-dependent functions can usually be approximated over a limited range of frequencies by functions of the form (8.5); over this range of frequencies, the magnitude Bode plot is approximately linear with slope 20n dB/decade.

A simple transferfunction whose magnitude is of the form (8.5) is thepoff at tiie origin:

(8.7)

The magnitude is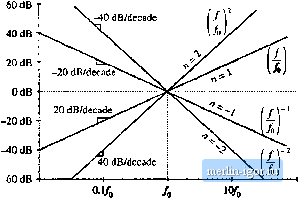

log scale

fig. Ю Magnitude Bode plou of functions wtiicfr vary as/ are Jiriear, with slope ii dB per decade.

- L L

If we define / = Ы2п and /у = №j2n, then Eq. (K.8) becomes

(8.9)

which is of the form of Eq. (8.5) with n = -1. As illustrated in Fig. 8.3, the magnitude Btxle plot of the pole at the origin (8.7) has a -20 dB per decade slope, and pas.scs through 0 dB at frcqucitcy/=/д.

8.1.1 Single Pule Re.sponse

Consider the simple R-C low-pass filter illustrated in Fig. 8.4. The transfer function is given by the voltage divider ratio

R -ЛЛг-

(S.IO)

This transfer function is a ratio of voltages, and hence is P P

dimensionless. By multiplying the numerator and denominator by sC, we can express the transfer function as a rational fraction:

(8.11)

The transfer function now coincides with the following staniiarii normalized form for a single pole:

(S.l 2)

The parameter 0) = 2n/g is found by equating the coefficients of j in the denominators of Eqs. (8.11) and (8.12). The result is

(8,13)

Since R and С are real positive quantities, Щ is also real and positive. The denominator of Eq. (8.12) contains a root at s = and hence G(.<i) contains a real pole in the left half of the complex plane.

To find the magnitude and phase of the transfer function, we let iyto, where; is the square root of-I. We then find the mag- 1тСС0 ш)) nitude and phase of the resulting complex-valued function. With s = >), Eq. (S.l2) becotnes

0(M =

1 iiO

(3.14)

The complex-valued G(/01) is illtistrated in Fig. 8.5, for one value of (0. The magnitude is

Re(G(/uJ))

ii 0(М ii = y[Rc(G(Jco))] + [lm (C(/o))p

(8,15)

Fig. 8.S Magnitude aiid phase of the complex-valued function Gijtii).

Here, we have assumed that (flo is real. In decibels, the magnitude is

lGOar)), = -201og, /тт()

(8.16)

The easy way to sketch the magnitude Bode plot of G is to investigate the asymptotic behavior for large and small frequency.

For small frequency, И u)(j and/-*:/o, it is true that

(8.17)

The (tt)/ul) term ofEq. (8.15) is therefore much smaller than 1, and hence Eq. (8.15) becomes

(8.18)

In decibels, the magnitude is approximately