274 Сотепег Тгапфг FuiiaioiLi

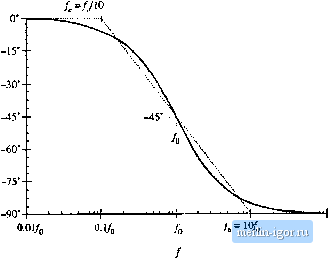Kig. 8.10 A .smipiei chiiice ( or Ibt aMirequency pliase asyiiiptulc, wliidi betier iipprnxiiiu)tes ilie curve; uvcr llic entire frequency range.

II СОш)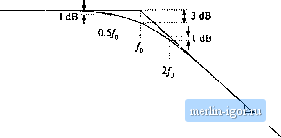

-20 dB/decade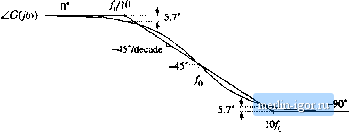

Fig. 8.f 1 Suinmary of the magnitude and philsi; Bode plni for llie single real pole.

+20 dB/decade

Fig. 8.12 Summafy of the magnitude and phase Bode plot for the single real zero.

пади,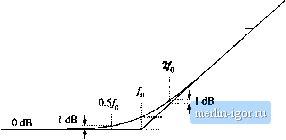

3. 3dB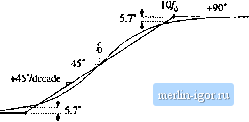

s.l,2 Single Zeru Respunse

A single zero response eotitaitis a rot>t in the iiumerattir ofthe transfer funetion, and can be written in the fc)llt)wing normalized form:

This transfer function hits magnitude

(8.29)

(8.30)

At Itnv frequency,/- /д = (iijht. the transfer functitin magnitude tends to 1 =Si 0 dB. At high frequency, f ff), the transfer function magnitude tends to ( 4), А.ч illustrated in Fig. 8,12, the high-frequency asymptote has slope +20 dB/decade. The phase is given by

ZC(;4i)) = tan

(8.31)

With the exception of a minu,4 sign, the phase is identical to Eq. (s.26). Hence, suitable asymptotes are as illustrated in Fig. s.12. The phase tends to 0 at low frequency, and to -н90° at high frequency. Over the interval/(/10 </< 1()/q, the pha.se asymptote has a slope of-H457decade.

Convener Тгапфг Fwictioni

Fig. 8.13 Summary of the magnltutlc and phase Bode plot for the real RHP zero.

+20 dB/decade

i[ cm I

0.5/

0 dB 1 dB .J.J-HTf 3 dB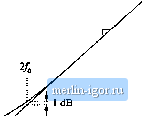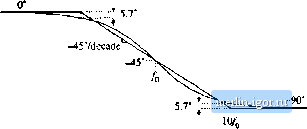

8.1 J Right Hair-Phine Zero

Right half-plane zeroes are often encountered in the small-signal transfer functions of switching converters. These terms have the following normalized form:

(8,32)

The root of Eq. (8.32) is positive, and hence lies in the right half of the complex .v-plane. The right half-plane zero is also sometimes called a nonmininium phase zero. Its normalized form, Eq. (8.32), resembles the normalized form of the (left half-plane) zero ofEq. (8.2У), with the exception of a minus sign in the coefficient of .т. The minus sign causes a phase reversal at high frequency. The transfer function has magnitude

(8.33)

This expression is identical to Eq. (8.30). Hence, it is impossible to distinguish a right half-plane zero from a left half-plane zero by the magnitude alone. The phase is given by

Z(7(;u)) = - tail

(8.34)

This coincides with the expression for the phase of the single pole, Eq. (8.26). So the right half-plane zero exhibits the magnitude response of the left half-plane zero, but the phase response of the pole. Magnitude and phase asymptotes are summarized in Fig. 8.13.