CHAPTER 2. FINITE AUTOMATA b

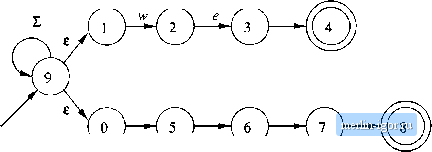Start e V У b v у a v у у

Figure 2.19; Using e-transitions to help recognize keywords

2.5.2 The Formal Notation for an e-NFA

We may represent an e-NFA exactly as we do an NFA, with one exception: the transition function must include information about transitions on e. Formally, we represent an e-NFA A by A - {Q,£,S,qo,F), where all components have their same interpretation as for an NFA, except that 5 is now a function that takes as arguments:

1, .A state in Q, and

2. A member of £ U {t}, that is, either an input symbol, or the symbol t. We require that the symbol for the empty string, cannot be a member of the alphabet E, so no confusion results.

Example 2.18: The e-NFA of Fig. 2.18 is represented formally as

E = ({go, 9b ,95}. { ,+!-, 0,1,..., 9}, г, go, {95}) where 6 is defined by the transition table in Fig. 2.20, □

Figure 2.20; Transition table for Fig. 2.18

2.5.3 Epsilon-Closures

We shall proceed to give formal definitions of an extended transit.i(m function for e-NFAs, which leads to the definition of acceptance of strings and languages by these automata, and eventually lets us explain why e-NFAs can be simulated by DFAs. However, we first need to learn a central definition, cahed the i-closure of a state. Informally, wo e-close a state g by following all transitions out of q that are labeled e. However, when we get to other states by following c, we follow the e-transitions out of those states, and so on, eventually finding every state that can be reacJied from q along any path whose arcs are all labeled e. Formally, we define the e-closure ECbOSE(g) recursively, as follows:

BASIS: State q is in eclose(g).

INDUCTION: If state p is in ECL0SE(9), and there is a transition from state p to state r labeled e, then r is in ECLOSE{g). More precisely, if S is the transition function of the e-NFA involved, and p is in ECL0Se{9), then ECLOSE{g) also contains aJl the states in S{p, e).

Example 2.19: For the automaton of Fig. 2.18, each stat(; is its own e-closure, with two exceptions: eclose{go) = {9o,9i} ani ECLO.Se((/;,) = {яз,Яо}- The reason is that there are only two e-transitions, one that adds gi to ECi.ose{go) and the other that adds q to EOLOSE(gy).

A more complex example is given hi Fig. 2.21. For tins collection of states, which may be part of some e-NFA, we can conclude that

ECLOSE(l) = {1,2,3,4,6}

Each of these states can be reached from state 1 along a path exclusively labeled e. For example, state 6 is reached by the path 1 2 3 -> 6. State 7 is not in eclose(I), since although it is reachable from .state 1, the path must иве the arc 4 5 that is not labeled e. The fact that state 6 is also reached from state 1 along a path 1 -> 4 -> 5 6 that has non-e transitions is unimportant. The existence of one path with all labels e is sufficient to show state 6 is in eclose(I). □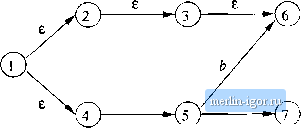

a г Figure 2.21: Some stat(!E and transitions

6{qo.e) eclose(go) = {gogi}-Compute S[qo,5) as follows:

1. First compute tlie transitions on hiput 5 from the states qo and qi that wc obtained in the calculation of S{qo,e), above. That is, wc compute 5(go,5) U 5(gi,5) = {qi,gA}.

2. Next, e-close the members of the set computed in step (1). We get ECLOSE(gi) и BCL0SE(g4) {qi} U {qi} = {ь}- That set is 5{qo,b). This two-step pattern repeats for the next two symbols.

2.5.4 Extended Transitions and Languages for e-NFAs

The e-closure allows us to explain easily what the transitions of an e-NFA look hke when given a sequence of (non-e) inputs. Prom there, we can define what it means for an e-NFA to accept its input.

Suppose that E = {Q, Г, 5, qo, F) is an e-NFA. We first define 6, the extended transition function, to reflect what happens on a sequence of inputs. The intent is that 5{q, w) is the set of states that can be reached along a path whose labels, when concatenated, form the string w. As always, es along this path do not contribute to w. The appropriate recursive definition of 6 is:

basis: S{q,e) = eclose(g), That is, if the label of the path is e, then wo can follow only f-laboled arcs extending from state q; that is exactly what eclose does.

INDUCTION: Suppose w is of the form xa, where a is the last symbol of w. Note that a is a member of S; it cannot be (, which is not in S, We compute S{q, w) as fofiows:

1. Let {pi ,p2, ;Pfc} be 5{q, x). That is, the pis are all and only the states that we can reach from q following a path labeled x. This path may end with one or more transitions labeled e, and may have other e-transitions, as well.

2. Let UJL,! 5{pi, a) be the set {rj, 2,..., }. That is, follow all transitions labeled a from states we сгт reach from q along paths labeled x. The Tjs are some of the states we can reach from q along paths labeled w. The additional states we can reach are found from the rs by following e-labeled arcs in step (3), below.

3. Then 6iq,w) - Uli bclose(rj). This additional closure step includes all the paths from q labeled iv, by considering the possibility that there are additional e-labcled arcs that we can follow after making a transition on the final real symbol, a.

Example 2.20: Let us compute S{qo,5.6) for the e-NFA of Fig. 2.18, A summary of the steps needed are as follows: